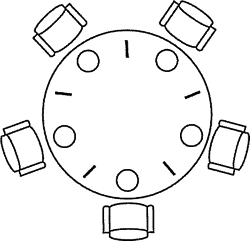
哲学家进餐问题(Dining philosophers problem)

发表于 更新于 分类于 ， ， ， ， Disqus：

哲学家就餐问题可以这样表述，假设有五位哲学家围坐在一张圆形餐桌旁，做以下两件事情之一：吃饭，或者思考。吃东西的时候，他们就停止思考，思考的时候也停止吃东西。餐桌中间有一大碗意大利面，每位哲学家之间各有一支餐叉。因为用一支餐叉很难吃到意大利面，所以假设哲学家必须用两支餐叉吃东西。他们只能使用自己左右手边的那两支餐叉。哲学家就餐问题有时也用米饭和五根筷子而不是意大利面和餐叉来描述，因为吃米饭必须用两根筷子。
如何设计一套规则，使得在哲学家们在完全不交谈，也就是无法知道其他人可能在什么时候要吃饭或者思考的情况下，可以在这两种状态下永远交替下去。

假设我们要求哲学家遵守以下规则：

1. 哲学家在左边的叉子可用（没有其他人拿起）之前处于思考状态。如果左边的叉子可用，就拿起来。
2. 哲学家等待右边的叉子可用。如果右边的叉子可用，就拿起来。
3. 如果两个叉子都已经拿起来，开始吃意大利面，每次吃面都花费同样的时间。
4. 吃完后先放下左边的叉子。
5. 然后放下右边的叉子。
6. 开始思考（进入一个循环）

1
2
3
4
5
6
7
8
9
10
11
	semaphore chopstick[5] = {1,1,1,1,1}; //定义信号量数组chopstick[5],并初始化
Pi(){  //i号哲学家的进程
	while(1){
		P(chopstick[i]); //取左边筷子
		P(chopstick[(i+1)%5]);  //取右边篌子
		eat;
		V(chopstick[i]); //放回左边筷子
		V(chopstick[(i+1)%5]);  //放回右边筷子
		think;
	}
}

这个解法是失败的，当每个哲学家都拿起左侧的叉子，等待右侧的叉子可用时，就会进入死锁状态，每个哲学家将永远都在等待（右边的）另一个哲学家放下叉子。

正确的解法

  • 解法一
    假设当一个哲学家左右两边的筷子都可用时，才允许他抓起筷子。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
semaphore chopstick[5] = {1,1,1,1,1}; //初始化信号量
semaphore mutex=l;  //设置取筷子的信号量

Pi(){ //i号哲学家的进程
	while(1){
		P(mutex); //在取筷子前获得互斥量，一次只能由一个哲学家取筷子
		P(chopstick[i]) ; //取左边筷子
		P(chopstick[(i+1)%5]);  //取右边筷子
		V(mutex); //释放取筷子的信号量
		eat;
		V(chopstick[i]);  //放回左边筷子
		V(chopstick[(i+1)%5]);  //放回右边筷子
		think;
	}
}
  • 解法二
    至多只允许有四位哲学家同时去拿左边的筷子，最终能保证至少有一位哲学家能够进餐，并在用完时能释放出他用过的两只筷子，从而使更多的哲学家能够进餐。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
semaphore chopstick[5] = {1,1,1,1,1}; //初始化信号量
semaphore eating = 4;  //至多只允许四个哲学家可以同时进餐

Pi(){ //i号哲学家的进程
	while(1){
		think;
		P(eating); //请求进餐，若是第五个则挨饿
		P(chopstick[i]); //取左边筷子
		P(chopstick[(i+1)%5]) ;  //取右边筷子
		eat;
		V(chopstick[(i+1)%5]) ;  //放回右边筷子
		V(chopstick[i]) ;  //放回左边筷子
		V(eating); //释放信号量给其他挨饿的哲学家
	}
}
  • 解法三
    仅当哲学家的左右两只筷子均可使用，才允许他拿起筷子进餐。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
semaphore chopstick[5] = {1,1,1,1,1}; //初始化信号量
semaphore mutex = 1;  //设置取筷子的信号量

Pi(){ //i号哲学家的进程
	while(1){
		think;
		P(mutex); //在去筷子前获得互斥量
		P(chopstick[i]); //取左边筷子
		P(chopstick[(i+1)%5]) ;  //取右边筷子
		V(mutex); //释放互斥量
		eat;
		V(chopstick[(i+1)%5]) ;  //放回右边筷子
		V(chopstick[i]) ;  //放回左边筷子

	}
}
  • 解法四
    规定奇数号哲学家先拿他左边的筷子，然后在去拿右边的筷子；而偶数号哲学家则相反。按此规定，将是1、2号哲学家竞争1号筷子；3、4号哲学家竞争3号筷子。

即5位哲学家都先竞争奇数号筷子，获得后，再去竞争偶数号筷子，最后总会有一位哲学家能够获得两只筷子而进餐。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
semaphore chopstick[5] = {1,1,1,1,1}; //初始化信号量

Pi(){ //i号哲学家的进程
	while(1){
		think;
		if(i%2==0){
			P(chopstick[(i+1)%5]) ;  //取右边筷子
			P(chopstick[i]); //取左边筷子
			eat;
			V(chopstick[(i+1)%5]) ;  //放回右边筷子
			V(chopstick[i]) ;  //放回左边筷子
		}else{	   //奇数哲学家，先左后右
			P(chopstick[i]); //取左边筷子
			P(chopstick[(i+1)%5]) ;  //取右边筷子
			V(mutex); //释放互斥量
			eat;
			V(chopstick[i]) ;  //放回左边筷子
			V(chopstick[(i+1)%5]) ;  //放回右边筷子

		}
	}
}
  • 解法五
    采用AND型信号量机制来解决，即要求每个哲学家先获得两个临界资源（筷子）后方能进餐。
1
2
3
4
5
6
7
8
9
10
11
semaphore chopstick[5] = {1,1,1,1,1}; //初始化信号量
semaphore mutex = 1;  //设置取筷子的信号量

Pi(){
	while(1){
		think;
		P(chopstick[i],chopstick[(i+1)%5]);
		eat;
		V(chopstick[i],chopstick[(i+1)%5]);
	}
}